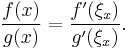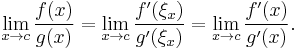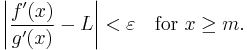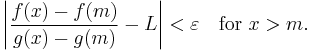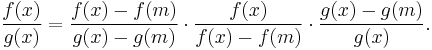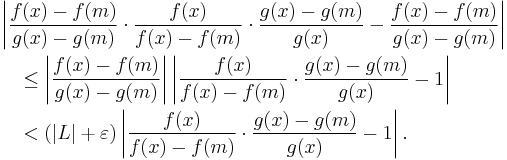L'Hôpital's rule
In calculus, l'Hôpital's rule (also called Bernoulli's rule) uses derivatives to help evaluate limits involving indeterminate forms. Application (or repeated application) of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital, who published the rule in his book Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes (literal translation: Analysis of the Infinitely Small to Understand Curved Lines) (1696), the first textbook on differential calculus.[1] However, it is believed that the rule was discovered by the Swiss mathematician Johann Bernoulli.[2]
The Stolz-Cesàro theorem is a similar result involving limits of sequences, but it uses finite difference operators rather than derivatives.
In its simplest form, l'Hôpital's rule states that for functions ƒ and g:
If 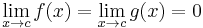 or
or 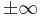 and
and 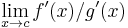 exists,
exists,
then 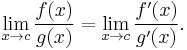
The differentiation of the numerator and denominator often simplifies the quotient and/or converts it to a determinate form, allowing the limit to be evaluated more easily.
Contents |
General form
The general form of l'Hôpital's rule covers many more cases. Suppose that c and L are extended real numbers (i.e., real numbers, positive infinity, or negative infinity). Suppose that either
or
And suppose that
Then
The limits may also be one-sided limits.
Requirement that limit exists
The requirement that the limit
exists is essential. Differentiation of indeterminate forms can sometimes lead to limits that do not exist. If this happens, then l'Hôpital's rule does not apply. For example, if ƒ(x) = x + sin(x) and g(x) = x, then
which does not exist, whereas
Examples
- Here is an example involving the sinc function and the indeterminate form 0/0:
- Alternatively, just observe that the limit is the definition of the derivative of the sine function at zero.
- This is a more elaborate example involving 0/0. Applying l'Hôpital's rule a single time still results in an indeterminate form. In this case, the limit may be evaluated by applying the rule three times:
- This example involves 0/0. Suppose that b > 0. Then
- Here is another example involving 0/0:
- This example involves ∞/∞. Assume
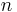 is a positive integer. Then
is a positive integer. Then
- Repeatedly apply l'Hôpital's rule until the exponent is zero to conclude that the limit is zero.
- Here is another example involving ∞/∞:
- Here is an example involving the impulse response of a raised-cosine filter and 0/0:
- One can also use l'Hôpital's rule to prove the following theorem. If
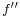 is continuous at x, then
is continuous at x, then
- Sometimes L'Hôpital's rule is invoked in a tricky way: suppose
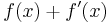 converges as
converges as 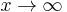 . It follows:
. It follows: - :
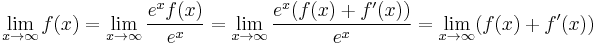
-
- and so
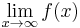 exists and
exists and 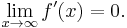
- and so
Other indeterminate forms
Other indeterminate forms, such as 1∞, 00, ∞0, 0·∞, and ∞ − ∞, can sometimes be evaluated using l'Hôpital's rule. For example, to evaluate a limit involving ∞ − ∞, convert the difference of two functions to a quotient:
where l'Hôpital's rule was applied in going from (1) to (2) and then again in going from (3) to (4).
l'Hôpital's rule can be used on indeterminate forms involving exponents by using logarithms to "move the exponent down". Here is an example involving the indeterminate form 00:
It is valid to move the limit inside the exponential function because the exponential function is continuous. Now the exponent 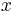 has been "moved down". The limit
has been "moved down". The limit 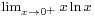 is of the indeterminate form 0·(−∞), but as shown in an example above, l'Hôpital's rule may be used to determine that
is of the indeterminate form 0·(−∞), but as shown in an example above, l'Hôpital's rule may be used to determine that
Thus
Other methods of evaluating limits
Although l'Hôpital's rule is a powerful way of evaluating otherwise hard-to-evaluate limits, it is not always the easiest way. Consider
This limit may be evaluated using l'Hôpital's rule:
It is valid to move the limit inside the cosine function because the cosine function is uniformly continuous.
Another way to evaluate this limit is to use a substitution. Let y = 1/x. As |x| approaches infinity, y approaches zero. So,
The final limit may be evaluated using l'Hôpital's rule or by noting that it is the definition of the derivative of the sine function at zero.
Still another way to evaluate this limit is to use a Taylor series expansion:
For |x| ≥ 1, the expression in parentheses is bounded, so the limit in the last line is zero.
Logical circularity
In some cases it may constitute circular reasoning to use l'Hôpital's rule to evaluate a limit. Consider
If the purpose of evaluating this limit is to prove that if ƒ(x) = xn, then
and one uses l'Hôpital's rule and this same fact to evaluate the limit, then the argument uses the conclusion as an assumption (i.e., begging the question) and is therefore fallacious (even though the conclusion is true).
Case where ƒ and g are differentiable at c
The proof of l'Hôpital's rule is simple in the case where ƒ and g are differentiable at the point c. It is not a proof of the general l'Hôpital's rule because it requires stronger hypotheses than does l'Hôpital's rule, namely, the differentiability of ƒ and g at c.
Suppose that ƒ and g are continuous and differentiable at c, ƒ(c) = g(c) = 0, and g′(c) ≠ 0. Then
(remember that ƒ(c) = g(c) = 0). This follows from the limit rules for quotients and the definition of the derivative.
This suggests the general case of l'Hôpital's rule, which does not require the functions ƒ and g to be differentiable at the point c and is proven below.
Geometric interpretation
Consider curve in the plane whose x-coordinate is given by g(t) and whose y-coordinate is given by ƒ(t) – i.e.
Suppose ƒ(c) = g(c) = 0. The limit of the ratio ƒ(t)/g(t) as t → c is the slope of tangent to the curve at the point [0, 0]. The tangent to the curve at the point t is given by ![[g'(t),f'(t)]](/I/1107df0ec4e7843bffefbbf5ea2ed3de.png) . L'Hôpital's rule then states that the slope of the tangent at 0 is the limit of the slopes of tangents at the points approaching 0.
. L'Hôpital's rule then states that the slope of the tangent at 0 is the limit of the slopes of tangents at the points approaching 0.
Proof of l'Hôpital's rule
A standard proof of l'Hôpital's rule uses Cauchy's mean value theorem. l'Hôpital's rule has many variations depending on whether c and L are finite or infinite, whether ƒ and g converge to zero or infinity, and whether the limits are one-sided or two-sided. All the variations follow from the two main variations below without, for the most part, requiring any new reasoning.[3]
Zero over zero
Suppose that c and L are finite and ƒ and g converge to zero.
First, define (or redefine) ƒ(c) = 0 and g(c) = 0. This makes ƒ and g continuous at c, but does not change the limit (since, by definition, the limit does not depend on the value at the point c). Since 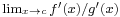 exists, there is an interval (c − δ, c + δ) such that for all x in the interval, with the possible exception of x = c, both
exists, there is an interval (c − δ, c + δ) such that for all x in the interval, with the possible exception of x = c, both 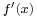 and
and  exist and
exist and  is not zero.
is not zero.
If x is in the interval (c, c + δ), then the mean value theorem and Cauchy's mean value theorem both apply to the interval [c, x] (and a similar statement holds for x in the interval (c − δ, c)). The mean value theorem implies that g(x) is not zero (since otherwise there would be a y in the interval (c, x) with 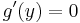 ). Cauchy's mean value theorem now implies that there is a point ξx in (c, x) such that
). Cauchy's mean value theorem now implies that there is a point ξx in (c, x) such that
If x approaches c, then ξx approaches c (by the squeeze theorem ). Since 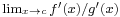 exists, it follows that
exists, it follows that
Infinity over infinity
Suppose that L is finite, c is positive infinity, and ƒ and g converge to positive infinity.
For every ε > 0, there is an m such that
The mean value theorem implies that if x > m, then g(x) ≠ g(m) (since otherwise there would be a y in the interval (m, x) with 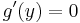 ). Cauchy's mean value theorem applied to the interval [m, x] now implies that
). Cauchy's mean value theorem applied to the interval [m, x] now implies that
Since ƒ converges to positive infinity, if x is large enough, then ƒ(x) ≠ ƒ(m). Write
Now,
For x sufficiently large, this is less than ε and therefore
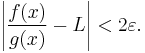 *
*
- Note: Steps are missing.
See also
Notes
- ↑ O'Connor, John J.; Robertson, Edmund F. "De_L'Hopital biography". The MacTutor History of Mathematics archive. Scotland: School of Mathematics and Statistics, University of St Andrews. http://www-history.mcs.st-andrews.ac.uk/Biographies/De_L'Hopital.html. Retrieved 21 December 2008.
- ↑ Weisstein, Eric W., "L'Hospital's Rule" from MathWorld.
- ↑ Spivak, Michael (1994). Calculus. Houston, Texas: Publish or Perish. pp. 201–202, 210–211. ISBN 0-914098-89-6.
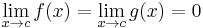
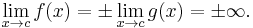
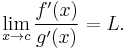
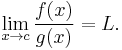
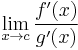
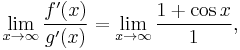
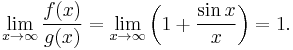
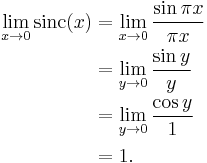
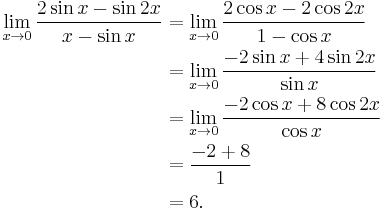
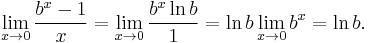
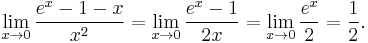
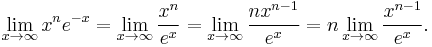
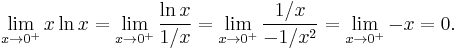
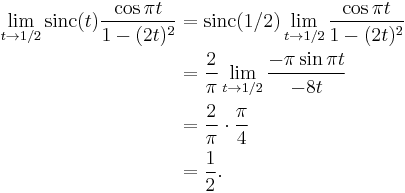
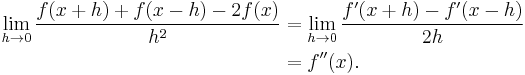
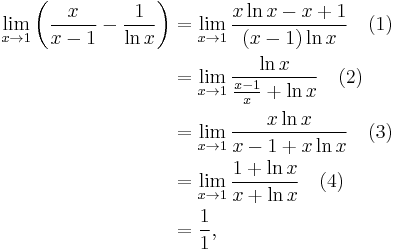
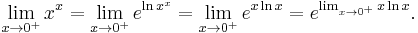
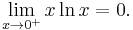
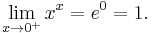
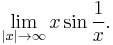
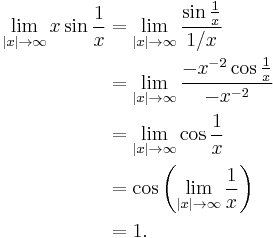
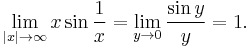
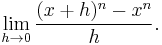
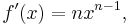
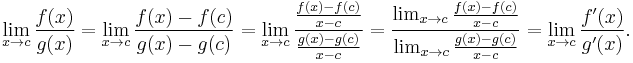
![t\mapsto [g(t),f(t)]. \,](/I/12c1e64fd84c6a461d37569359ccf14a.png)